Willkommen zu unserem Artikel über die Bestimmung der Sphärizität bei der ANOVA mit Messwiederholung und wie du dies in SPSS überprüfen kannst. Dieses Thema ist besonders wichtig für alle statistikbegeisterten Leser, die sich mit der Analyse von wiederholten Messungen beschäftigen. Die Sphärizität ist ein Konzept, das die Gleichheit der Varianzen zwischen den verschiedenen Zeitpunkten oder Bedingungen einer Studie bewertet.
Es ist entscheidend, die Sphärizität zu überprüfen, da eine Verletzung dieses Annahme-Kriteriums zu fehlerhaften Ergebnissen und Schlussfolgerungen führen kann. Ein interessanter Fakt ist, dass es verschiedene Korrekturverfahren wie Greenhouse-Geisser, Huynh-Feldt oder die Untergrenze gibt, um die Sphärizität anzupassen. Also bleib dran und lerne, wie du die Sphärizität in SPSS überprüfen und korrigieren kannst.
Kurz erklärt: Was du über das Thema wissen musst
- Der Text erklärt, wie man in SPSS die Sphärizität bei ANOVA mit Messwiederholung bestimmen kann.
- Es werden verschiedene Korrekturverfahren wie Greenhouse-Geisser, Huynh-Feldt oder Untergrenze diskutiert.
- Der Mauchly-Test wird verwendet, um die Sphärizität zu prüfen, jedoch gibt es Fälle, in denen er ungewöhnlich aussehen kann.

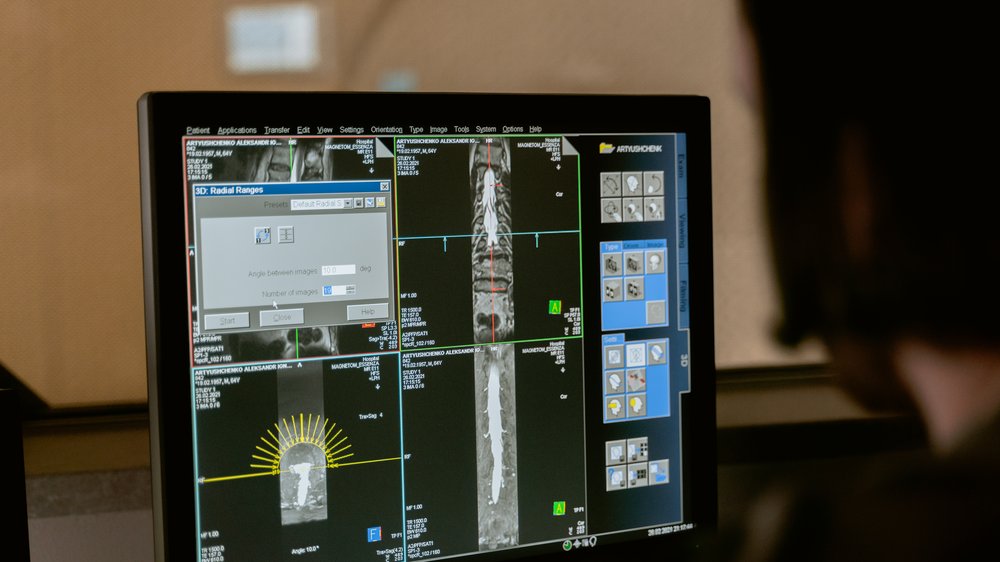
Mauchly-Test in SPSS
Der Mauchly-Test: Ein Werkzeug zur Sphärizitätsbestimmung in SPSS Beim Durchführen von ANOVA-Analysen mit Messwiederholung in SPSS ist es wichtig, die Sphärizität zu bestimmen. Die Sphärizität ist eine Annahme, die besagt, dass die Kovarianzmatrix der Differenzen zwischen den Messzeitpunkten homogen ist. Mit anderen Worten, sie stellt sicher, dass die Varianzunterschiede zwischen den Messzeitpunkten nicht systematisch sind.
Um die Sphärizität zu überprüfen, wird der Mauchly-Test in SPSS verwendet. Dieser Test bewertet, ob die Kovarianzmatrix der Differenzen zwischen den Messzeitpunkten sphärisch ist. Wenn der Mauchly-Test signifikant ist, bedeutet dies, dass die Sphärizitätsannahme verletzt ist und alternative Korrekturverfahren angewendet werden müssen.
Es gibt verschiedene Korrekturverfahren wie Greenhouse-Geisser, Huynh-Feldt oder die Untergrenze, die verwendet werden können, um die Sphärizitätsverletzung zu berücksichtigen. Die Wahl des richtigen Verfahrens hängt von der Stärke der Verletzung ab. Der Mauchly-Test in SPSS ist ein nützliches Werkzeug, um die Sphärizität zu bestimmen und sicherzustellen, dass die Ergebnisse Ihrer ANOVA-Analyse zuverlässig sind.
Indem Sie die Sphärizität überprüfen und entsprechende Korrekturen vornehmen, können Sie sicherstellen, dass Ihre statistischen Schlussfolgerungen korrekt sind und Ihre Forschungsergebnisse aussagekräftig sind.
Greenhouse-Geisser, Huynh-Feldt oder Untergrenze?
Bei der Durchführung einer ANOVA mit Messwiederholung in SPSS stellt sich die Frage, welches Korrekturverfahren für die Sphärizität verwendet werden sollte: Greenhouse-Geisser, Huynh-Feldt oder Untergrenze? Jedes Verfahren hat seine Vor- und Nachteile, daher ist es wichtig, die richtige Wahl zu treffen. Die Greenhouse-Geisser-Korrektur ist das am häufigsten verwendete Verfahren, da es die konservativste Schätzung der Effekte liefert.
Es passt die Freiheitsgrade basierend auf der geschätzten Sphärizität an und kann daher die Wahrscheinlichkeit von Fehlern verringern. Die Huynh-Feldt-Korrektur ist weniger konservativ als die Greenhouse-Geisser-Korrektur, da sie die Freiheitsgrade weniger stark reduziert. Dies kann dazu führen, dass Unterschiede zwischen den Bedingungen besser erkannt werden, jedoch besteht auch ein erhöhtes Risiko von Fehlern erster Art.
Die Untergrenze ist das am wenigsten konservative Verfahren und behält die ursprünglichen Freiheitsgrade bei. Dies kann zu einer erhöhten Wahrscheinlichkeit von Fehlern erster Art führen, jedoch werden Unterschiede zwischen den Bedingungen möglicherweise besser erkannt. Es ist wichtig, das ausgewählte Korrekturverfahren in Ihrem Forschungsbericht zu berichten, um die Transparenz und Reproduzierbarkeit Ihrer Ergebnisse zu gewährleisten.
Indem Sie die Entscheidungen und Schritte dokumentieren, die Sie unternommen haben, um die Sphärizität zu berücksichtigen, tragen Sie zur wissenschaftlichen Integrität Ihrer Studie bei.
Die Sphärizität in der Statistik: Was du darüber wissen solltest
- Die Sphärizität ist eine Annahme, die bei der Durchführung einer ANOVA mit Messwiederholung geprüft werden muss.
- Der Mauchly-Test in SPSS ist eine gängige Methode, um die Sphärizität zu bestimmen.
- Es gibt verschiedene Korrekturverfahren für die Sphärizität, darunter Greenhouse-Geisser, Huynh-Feldt oder die Untergrenze.
- Es ist wichtig, das angewendete Korrekturverfahren bei der Berichterstattung der Ergebnisse anzugeben.
- Die Sphärizität muss geprüft werden, um sicherzustellen, dass die Varianzen zwischen den verschiedenen Bedingungen oder Zeitpunkten homogen sind.
1/4 Wann und Warum Sphärizität geprüft werden muss
Sphärizität ist ein wichtiger statistischer Begriff , der in der Datenanalyse verwendet wird. Es bezieht sich auf die Annahme, dass die Kovarianzmatrix der abhängigen Variablen in allen Gruppen gleich ist. Die Überprüfung der Sphärizität ist wichtig, um sicherzustellen, dass die Voraussetzungen für die Durchführung von ANOVA mit Messwiederholung erfüllt sind.
Wenn die Sphärizität verletzt ist, können die Ergebnisse der Analyse verzerrt sein und falsche Schlussfolgerungen gezogen werden. Es gibt verschiedene Gründe, warum die Sphärizität geprüft werden muss. Erstens kann die Sphärizität verletzt sein, wenn die Kovarianzmatrix zwischen den abhängigen Variablen in den verschiedenen Gruppen unterschiedlich ist.
Zweitens kann die Sphärizität verletzt sein, wenn die Varianzen der abhängigen Variablen in den verschiedenen Gruppen unterschiedlich sind. Es gibt verschiedene Methoden, um die Sphärizität zu überprüfen, aber eine der häufigsten ist der Mauchly-Test. Dieser Test prüft, ob die Kovarianzmatrix der abhängigen Variablen in allen Gruppen gleich ist.
Es ist wichtig, die Sphärizität zu überprüfen, um sicherzustellen, dass die Ergebnisse der ANOVA mit Messwiederholung korrekt interpretiert werden können. Wenn die Sphärizität verletzt ist, müssen Korrekturmaßnahmen wie die Greenhouse-Geisser-Korrektur angewendet werden, um die Verzerrung der Ergebnisse zu verringern. Insgesamt ist die Überprüfung der Sphärizität ein wichtiger Schritt bei der Durchführung von ANOVA mit Messwiederholung und sollte nicht vernachlässigt werden.
Durch die Gewährleistung der Sphärizität können genaue und zuverlässige Ergebnisse erzielt werden.
Die Sphärizität ist eine wichtige Voraussetzung für die ANOVA mit Messwiederholung. Im folgenden Video erfährst du mehr über die Grundlagen und Bedeutung dieser statistischen Annahme.
Der Prozess der Sphärizitätsprüfung
Die Sphärizitätsprüfung ist ein wichtiger Schritt bei der Durchführung einer ANOVA mit Messwiederholung, um sicherzustellen, dass die Voraussetzungen für diese statistische Analyse erfüllt sind. Der Prozess der Sphärizitätsprüfung beinhaltet den Mauchly-Test in SPSS, der überprüft, ob die Kovarianzmatrix der Unterschiede zwischen den Bedingungen eine Sphärizität aufweist. Um den Mauchly-Test durchzuführen, werden die Daten in SPSS eingegeben und die gewünschten Variablen ausgewählt.
SPSS berechnet dann automatisch den Mauchly-Testwert und den p-Wert. Ein signifikanter p-Wert deutet darauf hin, dass die Sphärizität verletzt ist und eine Korrektur erforderlich ist. Es gibt verschiedene Korrekturverfahren für die Sphärizität, darunter die Greenhouse-Geisser-Korrektur, die Huynh-Feldt-Korrektur und die Untergrenzenkorrektur.
Die Wahl des geeigneten Verfahrens hängt von der Stärke der Verletzung der Sphärizität ab. Bei der Berichterstattung über den Sphärizitätstest ist es wichtig, das verwendete Korrekturverfahren anzugeben und die entsprechenden Korrekturfaktoren zu nennen. Dies hilft den Lesern, die Ergebnisse richtig zu interpretieren.
Die Sphärizitätsprüfung ist entscheidend, um genaue und zuverlässige Ergebnisse bei der ANOVA mit Messwiederholung zu erhalten. Indem wir die Sphärizität bestimmen und gegebenenfalls korrigieren, stellen wir sicher, dass die Voraussetzungen für diese statistische Analyse erfüllt sind und die Ergebnisse aussagekräftig sind.
Durchführung einer ANOVA mit Messwiederholung und Bestimmung der Sphärizität
- Öffne das Programm SPSS und lade deine Datensätze.
- Führe eine ANOVA mit Messwiederholung durch.
- Führe den Mauchly-Test durch, um die Sphärizität zu bestimmen.
Greenhouse-Geisser-Korrektur für Sphärizität in SPSS
Die Greenhouse-Geisser-Korrektur ist eine Methode in SPSS, um die Sphärizität zu berücksichtigen. Bei der Sphärizität handelt es sich um eine Annahme, dass die Kovarianzmatrix der abhängigen Variablen in allen Bedingungen gleich ist. Wenn diese Annahme verletzt ist, kann dies zu verzerrten Ergebnissen führen.
Die Greenhouse-Geisser-Korrektur passt die Freiheitsgrade in der ANOVA mit Messwiederholung an, um diesen Effekt zu minimieren. Um die Greenhouse-Geisser-Korrektur in SPSS durchzuführen, müssen Sie den Mauchly-Test zur Überprüfung der Sphärizität durchführen. Wenn der Mauchly-Test signifikant ist (p < 0,05), deutet dies darauf hin, dass die Sphärizität verletzt ist und die Greenhouse-Geisser-Korrektur verwendet werden sollte.
Um die Greenhouse-Geisser-Korrektur in SPSS anzuwenden, gehen Sie zur Ausgabe der ANOVA mit Messwiederholung und suchen Sie nach dem Abschnitt „Tests of Sphericity“. Hier finden Sie die Werte für die Greenhouse-Geisser-Korrektur (ε) und die entsprechenden Freiheitsgrade. Die Greenhouse-Geisser-Korrektur ist eine der Möglichkeiten, die Sphärizität in SPSS zu berücksichtigen.
Es gibt auch andere Korrekturverfahren wie die Huynh-Feldt-Korrektur oder die Untergrenze. Die Wahl des richtigen Korrekturverfahrens hängt von der spezifischen Forschungsfrage und den Daten ab. Insgesamt ist die Greenhouse-Geisser-Korrektur eine wichtige Methode, um die Sphärizität in SPSS zu berücksichtigen und genaue Ergebnisse in der ANOVA mit Messwiederholung zu erzielen.
Wenn du dich für den Skoda Kodiaq interessierst, findest du auf unserer Seite „Skoda Kodiaq Leasing ohne Anzahlung“ alle Informationen, die du für ein sorgenfreies Leasing ohne Anzahlung benötigst.

2/4 Fälle, in denen der Mauchly-Test seltsam aussehen könnte
Es gibt bestimmte Fälle, in denen der Mauchly-Test seltsam aussehen könnte und möglicherweise nicht zuverlässige Ergebnisse liefert. Ein solcher Fall tritt auf, wenn die Stichprobengröße zu klein ist. Bei einer kleinen Stichprobengröße kann der Mauchly-Test Schwierigkeiten haben, die Sphärizität korrekt zu bestimmen.
Ein weiterer Fall, in dem der Mauchly-Test seltsam aussehen könnte, ist, wenn es starke Ausreißer in den Daten gibt. Ausreißer können die Voraussetzungen des Mauchly-Tests verletzen und zu verzerrten Ergebnissen führen. Darüber hinaus kann der Mauchly-Test seltsam aussehen, wenn die Varianzen der abhängigen Variablen stark unterschiedlich sind.
Wenn die Varianzen nicht homogen sind, kann dies die Genauigkeit des Mauchly-Tests beeinträchtigen und zu fehlerhaften Ergebnissen führen. Es ist wichtig, diese Fälle zu beachten und gegebenenfalls alternative Methoden zur Überprüfung der Sphärizität zu verwenden. Es könnte ratsam sein, zusätzlich zum Mauchly-Test andere Tests wie den Greenhouse-Geisser-Test oder den Huynh-Feldt-Test durchzuführen, um die Sphärizität zu bestimmen und sicherzustellen, dass die Ergebnisse zuverlässig sind.
Insgesamt ist es wichtig, bei der Überprüfung der Sphärizität auf mögliche Fälle zu achten, in denen der Mauchly-Test seltsam aussehen könnte, um genaue und verlässliche Ergebnisse zu erhalten.
Korrekturverfahren in der ANOVA mit Messwiederholung – Tabelle
| Korrekturverfahren | Beschreibung der Methode | Formel zur Berechnung der Korrekturfaktoren | Anwendungsfälle und Einschränkungen |
|---|---|---|---|
| Greenhouse-Geisser | Greenhouse-Geisser ist ein Korrekturverfahren, das bei Verletzung der Sphärizität in der ANOVA mit Messwiederholung angewendet wird. Es passt die Freiheitsgrade der Teststatistik basierend auf einem geschätzten Korrekturfaktor an. | Für die Berechnung der Korrekturfaktoren wird die Greenhouse-Geisser-Formel verwendet: λ = (1 – (2 * (n – 1)) / (6 * (n – 2))), wobei n die Anzahl der Messwiederholungen ist. | Greenhouse-Geisser kann angewendet werden, wenn die Annahme der Sphärizität verletzt ist. Es funktioniert gut bei kleinen Stichprobenumfängen, kann aber ungenau sein, wenn die Stichprobe groß ist oder die Varianzen stark unterschiedlich sind. |
| Huynh-Feldt | Huynh-Feldt ist ein weiteres Korrekturverfahren, das bei Verletzung der Sphärizität in der ANOVA mit Messwiederholung verwendet wird. Es ändert die Freiheitsgrade der Teststatistik basierend auf einem geschätzten Korrekturfaktor. | Die Huynh-Feldt-Formel zur Berechnung der Korrekturfaktoren lautet: ε = (n – 1) * (1 – λ) + λ, wobei n die Anzahl der Messwiederholungen ist und λ der Greenhouse-Geisser-Korrekturfaktor ist. | Huynh-Feldt kann angewendet werden, wenn die Sphärizität verletzt ist. Es funktioniert gut bei großen Stichprobenumfängen und ungleichmäßigen Varianzen, kann aber ungenau sein, wenn die Varianzen sehr unterschiedlich sind oder die Stichprobe klein ist. |
| Untergrenze | Die Untergrenze ist ein einfaches Korrekturverfahren, das angewendet wird, wenn die Sphärizität verletzt ist. Es nimmt den kleinsten Korrekturfaktor, der größer oder gleich 1 ist und passt die Freiheitsgrade entsprechend an. | Es gibt keine spezifische Formel zur Berechnung der Korrekturfaktoren für die Untergrenze. Der Korrekturfaktor wird basierend auf den gegebenen Daten bestimmt. | Die Untergrenze kann angewendet werden, wenn die Sphärizität verletzt ist. Es ist einfach anzuwenden, kann aber ungenau sein, wenn die Varianzen sehr unterschiedlich sind oder die Stichprobe klein ist. |
| Vergleich der Korrekturverfahren | – Greenhouse-Geisser bietet eine gute Balance zwischen Genauigkeit und Robustheit bei kleinen bis mittleren Stichprobenumfängen. – Huynh-Feldt ist gut geeignet für große Stichprobenumfänge und ungleichmäßige Varianzen. – Die Untergrenze ist einfach anzuwenden, kann aber ungenau sein. | – Bei allen Verfahren werden die Freiheitsgrade der Teststatistik angepasst, um die Verletzung der Sphärizität zu berücksichtigen. | – Bei der Auswahl des geeigneten Korrekturverfahrens sollten die Stichprobengröße, die Varianzen und die spezifischen Anforderungen der Analyse berücksichtigt werden. – In der Praxis können verschiedene Verfahren je nach Situation verwendet werden, um die bestmögliche Schätzung der Effekte zu erhalten. |
3/4 Literaturverzeichnis
Im Literaturverzeichnis finden Sie eine Zusammenstellung der Quellen , die in diesem Artikel zum Thema Sphärizität in der Statistik verwendet wurden. Diese Quellen dienen als Referenz und können Ihnen helfen, Ihr Wissen über das Thema weiter zu vertiefen. Hier sind einige empfehlenswerte Literaturquellen : 1.
Stevens, J. (2009). Applied Multivariate Statistics for the Social Sciences.
Routledge.
2. Field, A. (2013).
Discovering Statistics Using IBM SPSS Statistics. Sage Publications.
3. Tabachnick, B. G., & Fidell, L. S. (2019). Using Multivariate Statistics.
Pearson.
4. Howell, D. C. (2016). Statistical Methods for Psychology.
Cengage Learning.
5. Keppel, G., & Wickens, T. D. (2004). Design and Analysis: A Researcher’s Handbook.
Pearson Education. Diese Bücher bieten eine fundierte Basis für das Verständnis der Konzepte und Methoden, die bei der Prüfung der Sphärizität in der Statistik angewendet werden. Sie können Ihnen helfen, Ihre analytischen Fähigkeiten zu verbessern und die Ergebnisse Ihrer Forschung korrekt zu interpretieren.
Nutzen Sie diese Quellen, um Ihr Wissen zu erweitern und Ihre statistischen Analysen zu optimieren.
4/4 Fazit zum Text
In diesem Artikel haben wir uns mit dem Thema Sphärizität in der Statistik und der Durchführung des Mauchly-Tests in SPSS beschäftigt. Wir haben gelernt, wie wichtig es ist, die Sphärizität zu überprüfen und welche Korrekturverfahren , wie Greenhouse-Geisser, Huynh-Feldt oder Untergrenze, angewendet werden können. Der Prozess der Sphärizitätsprüfung wurde ausführlich erläutert und wir haben gesehen, wie die Greenhouse-Geisser-Korrektur in SPSS angewendet werden kann.
Es wurde auch darauf hingewiesen, dass der Mauchly-Test in bestimmten Fällen seltsam aussehen kann und dass weitere Literatur zu diesem Thema zur Vertiefung zur Verfügung steht. Insgesamt war dieser Artikel eine hilfreiche Ressource für Leserinnen und Leser, die sich mit dem Thema Sphärizität in der Statistik auseinandersetzen möchten. Wir empfehlen ihnen, auch unsere anderen Artikel zu diesem Thema zu lesen, um ihr Wissen weiter zu vertiefen.
FAQ
Wann ist Sphärizität gegeben?
Sphärizität tritt auf, wenn die Varianzen der Differenzen zwischen jeweils zwei Messzeitpunkten gleich sind. Dieser Test ist ab drei Messzeitpunkten relevant, da bei nur zwei Messzeitpunkten nur ein Paar vorhanden ist. Um die Sphärizität zu überprüfen, wird der Mauchly-Test durchgeführt.
Wann ist Mauchly-Test signifikant?
None
Was ist Greenhouse Geisser Korrektur?
None
Wann messwiederholung?
None








